DFA minimieren
Auch wenn es mindestens die Hälfte meiner Leserschaft nicht wirklich interessieren wird, zeige ich hier mal wie man einen DFA per Hand (auch) minimieren kann. Das ist nämlich eigentlich recht einfach, solange der DFA simpel genug ist, wird aber oft genug kompliziert erklärt.
Nehmen wir folgenden DFA als zu minimierenden:
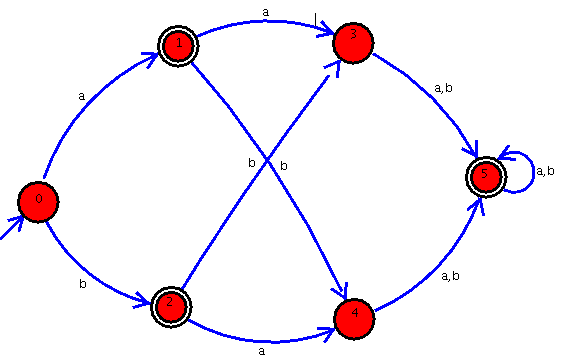
Minimieren kann nur funktionieren, wenn man überflüssige Zustände entfernt bzw. zusammenfasst. Am Anfang haben wir kein weiteres Unterscheidungsmerkmal als die Frage, ob die Zustände final sind (im Bild oben dargestellt durch die Doppelkreise) oder nicht. Grafisch betrachtet sieht das dann so aus (die Linien stellen die Übergänge dar, a ist blau, b braun, ab türkis)
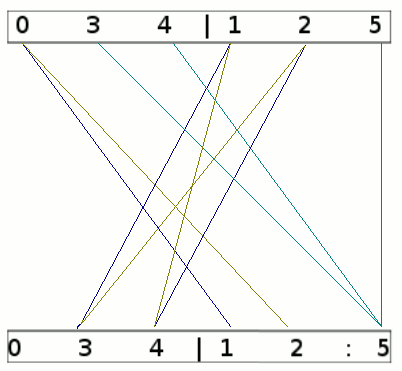
Der Doppelpunkt markiert das nächste Unterscheidungskriterium: Zustand 1 und 2 gehen über a bzw. b in die linke Gruppe, Zustand 5 geht jeweils in sich selbst, also in die rechte Gruppe: Hier kann innerhalb der Gruppe "125" nochmal unterschieden werden zwischen "12" (gehen beide in die linke Gruppe) und "5" (geht in die rechte Gruppe).
Nun sieht der nächste Schritt so aus:
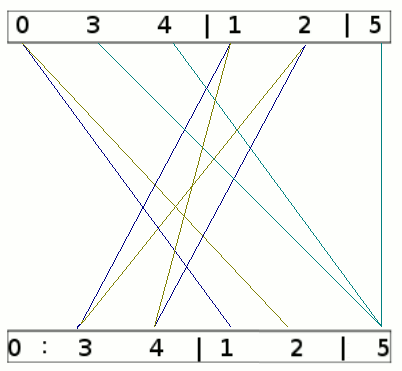
Da 3 und 4 nun auf eine andere Gruppe als 0 zeigen, kann jetzt auch in der linken Gruppe unterschieden werden.
Führt man das Verfahren nun nochmal aus, zeigt jedes Gruppenmitglied auf die gleiche Gruppe, ein weiteres Unterscheiden ist also nicht möglich.
Der fertig minimiert DFA sieht also wie folgt aus:
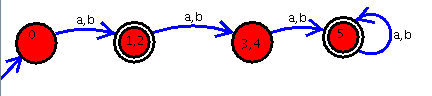
PS: Die DFAs wurden mit dem Automaton Simulator gezeichnet.
Nehmen wir folgenden DFA als zu minimierenden:

Minimieren kann nur funktionieren, wenn man überflüssige Zustände entfernt bzw. zusammenfasst. Am Anfang haben wir kein weiteres Unterscheidungsmerkmal als die Frage, ob die Zustände final sind (im Bild oben dargestellt durch die Doppelkreise) oder nicht. Grafisch betrachtet sieht das dann so aus (die Linien stellen die Übergänge dar, a ist blau, b braun, ab türkis)

Der Doppelpunkt markiert das nächste Unterscheidungskriterium: Zustand 1 und 2 gehen über a bzw. b in die linke Gruppe, Zustand 5 geht jeweils in sich selbst, also in die rechte Gruppe: Hier kann innerhalb der Gruppe "125" nochmal unterschieden werden zwischen "12" (gehen beide in die linke Gruppe) und "5" (geht in die rechte Gruppe).
Nun sieht der nächste Schritt so aus:

Da 3 und 4 nun auf eine andere Gruppe als 0 zeigen, kann jetzt auch in der linken Gruppe unterschieden werden.
Führt man das Verfahren nun nochmal aus, zeigt jedes Gruppenmitglied auf die gleiche Gruppe, ein weiteres Unterscheiden ist also nicht möglich.
Der fertig minimiert DFA sieht also wie folgt aus:

PS: Die DFAs wurden mit dem Automaton Simulator gezeichnet.
onli - 7. Jan, 19:54
leider hab ich gerade ein beispiel bei dem die pfeile meistens in 2 verschiedene gruppen zeigen.
kannst du mir da weiterhelfen?
Aufpassen muss man dann nur besonders darauf, dass sie nicht nur in die gleichen Gruppen zeigen, sondern dass auch jeweils das a in die gleiche Gruppe zeigen muss.
Zeigt 1 über a in 3 4, 2 aber über b in 3 4, dann kannst du 1 und 2 nicht zusammenfassen. Zeigt aber bei 1 und 2 a in 3 4 und das b zeigt auch jeweils in die gleiche Gruppe, dann kannst du die zusammenfassen.